« back

On the (in)security of ElGamal in OpenPGP - Part II

Authors: Luca De Feo, Bertram Poettering, Alessandro Sorniotti

Topics: side-channels, cryptanalysis

On the (in)security of ElGamal in OpenPGP - Part II #

This post continues the description of our work that analyses the security of the ElGamal public key encryption scheme in the OpenPGP context. In the previous post we discussed attacks targeting weak combinations of parameter choices and we saw how ciphertexts generated under those settings could be recovered easily.

This post describes instead attacks enabled by side-channels. While side-channel attacks are not new, we show here how the combination of insecure ElGamal configurations in some cases lowers the cost of the attack to the point of feasibility on commodity hardware. In particular, we present

In our paper we also present side-channel attacks against the modular exponentiation routines of crypto++ and Go which we do not review in this blog post.

Background #

Cache-based side-channel attacks #

The security of cryptographic protocols and schemes is often endangered in non-ideal settings where implementations leak additional information to the adversary. This is due to implementations unwillingly revealing information through side-effects that are observable in either the physical world (e.g. power consumption, noise, temperature) or the digital world (e.g. cache usage, execution time). Here we focus on the latter, and in particular, on attacks that target the CPU cache. We summarise here the salient points about this class of attacks and refer the reader to this, this or this article for further details.

Modern CPUs use a hierarchical memory architecture: fast, ephemeral memory with low capacity is backed by slower, permanent storage with higher capacity. Data is retrieved from storage and usually cached at all levels of the memory hierarchy until it’s available as input to the CPU gates (usually in registers) for the desired operations. CPU caches usually sit right before registers in said hierarchy, and are usually inclusive: when data is cached at a given cache level, it is also cached in lower levels. Also, given that the size of any level of cache is smaller than lower levels, including a datum in a cache usually involves evicting some other. Finally, data access times are vastly different based on whether and at which level a given datum is cached. These properties may be used to construct a side-channel, where observing the time it takes to access a specific datum reveals information about its (or other data’s) current caching status. This in turn reveals whether executing a specific piece of code required access to a specific datum. Crucially, if this datum relates to a cryptographic secret, this information may be revealed to an attacker.

As an example, consider the pseudocode below, containing the famous left-to-right square-and-multiply approach to modular exponentiation of base b to the power e modulo m.

1
2
3
4
5
6
7
8
9
10
11

function exponentiation(b, e, m)
x ← 1
for i ← |e| − 1 downto 0 do
	x ← x^2
	x ← x mod m
	if (e[i] = 1) then
		x ← x * b
		x ← x mod m
	endif
done
return x

If an attacker knew – for each round of the for loop – whether the condition of the if at line 5 is true, they would discover all the bits of the secret exponent. This information is conveyed through a cache side channel: for example, the code that implements multiplication (used at line 6) will be cached each time the condition is true, since that code needs to be executed.

A local attacker could extract this information using FLUSH+RELOAD: roughly speaking, the attacker would evict from the cache some portion of a target function (in our example, the function for the multiplication) at the beginning of each iteration of the loop, and would attempt to access it at the end. If the access time is below a certain threshold, it means that it was conceivably brought in the cache by an execution of the target of the conditional jump at line 5. This fact then leaks the bit at position i. Repeating the experiment for each round of the loop leaks the value of the exponent.

Modular exponentiation in Libgcrypt #

We target the function _gcry_mpi_powm of Libgcrypt at the version prior to commit 632d80ef3 (code).

1
2
3

void
_gcry_mpi_powm (gcry_mpi_t res,
                gcry_mpi_t base, gcry_mpi_t expo, gcry_mpi_t mod)

The function implements modular exponentiation of base raised to expo modulo mod. The result is stored in res.

Note that the _gcry_mpi_powm exponentiation routine is a little more involved than the simple square-and-multiply method sketched above: At a high level, instead of scanning the exponent bit by bit, it covers it with windows of bit-width at most W such that these windows, without overlapping, cover all the one-bits of the exponent. This technique is known as (left-to-right) sliding window exponentiation. After precomputing a small number of values, it can process one window at a time at the cost of a single multiplication (plus the squarings), thus offering a speed-up. For further information, see Handbook of Applied Cryptography, Algo 14.85.

In what follows we describe the salient parts of the implementation. As a first step, the _gcry_mpi_powm function determines window width W as follows (code):

1
2
3
4
5
6
7
8
9
10

if (esize * BITS_PER_MPI_LIMB > 512)
  W = 5;
else if (esize * BITS_PER_MPI_LIMB > 256)
  W = 4;
else if (esize * BITS_PER_MPI_LIMB > 128)
  W = 3;
else if (esize * BITS_PER_MPI_LIMB > 64)
  W = 2;
else
  W = 1;

Once the window size is determined, the function (code) goes on to precompute a table precomp as follows

1
2
3
4
5

for (i = 1; i < (1 << (W - 1)); i++)
{
	/* precomp[i] = base^(2 * i + 1) */
	...
}

Note that for all odd indices t between 1 and 2^W-1 the table compactly stores the value base^t. The main loop of the function (code) splits, left to right, the sequence of exponent bits into width-W windows that are linked by stretches of zeroes. More precisely, before each iteration of the loop (code) the bit-sequence e0 covered by a window, its length c0, and the length j of a window plus the length of the preceding stretch of zeroes is identified. The code then enters the for loop (code), whose main operations are summarised below.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

...
rp = res->d;
...
w.d = base_u;
...
for (j += W - c0; j >= 0; j--)
{
    ...
    for (k = 0; k < (1 << (W - 1)); k++)
    {
        ...
        u.d = precomp[k];
        mpi_set_cond (&w, &u, k == e0);
        ...
    }
    ...
    u.d = rp;
    mpi_set_cond (&w, &u, j != 0);
    mul_mod (xp, &xsize, rp, rsize, base_u, base_u_size,
                mp, msize, &karactx);
    ...
}
j = c0;

A picture is worth more than a thousand lines of code: the image below represents an exponent written in binary, and its decomposition into windows e₀, e₁, …, assuming W = 5. Ignore the color, for the moment.

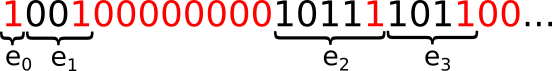
Windowed exponentation

In a nutshell, each iteration of the loop computes j times x ← x^2 and then x ← x * precomp[e0]. Note that, if this were implemented naively, executing the operations would give away, through cache side-channels, the nature of the operation (multiplication or squaring) and the index e0 used in the table look-up. The programmers of libgcrypt took precautions by implementing the table look-up in a more sophisticated way. First of all, the value of e0 is not leaked because i) each entry of the precomp table is accessed and ii) the mpi_set_cond is a secure version of a conditional memset() operation that hides whether the condition was true and hence whether the memory setting took place. Also, mul_mod is used for both the multiplication and the squaring since in the last iteration of the outer for loop, mpi_set_cond sets the second argument to coincide with the first.

Despite these precautions, considerable leakage can still be obtained by an attacker who can observe control flow dependent cache perturbations: in particular, the values j and c0 can be recovered by counting the number of iterations of the outer for loop in the figure above, since that loop is executed once per window. The bits in red in the picture above represent the leaked information: the position of each window is leaked by c0, and we know that each window must end with a 1 bit; additionally, when j > c0 we also learn a stretch of consecutive 0 bits.

Side channel based private key recovery in Libgcrypt #

We consider a victim process that uses a private key to decrypt ElGamal ciphertexts. The process uses an unpatched version of Libgcrypt that suffers from the issues described in the previous section. Given that we target cache side channels, the attacker may either be local, or it may be running on a different, co-located, VM. The former may target any cache level, the latter may only target LLC. Without loss of generality we conduct the exploitation against the L1 cache, and we use FLUSH+RELOAD on the shared (physical) data pages that host the Libgcrypt shared object.

Here we discuss how the adversary is able to determine the number of iterations of the square/multiply loop (for each window) and how this information may be employed towards recovering the secret exponent.

Obtaining the leakage #

The attacker may obtain the leakage by monitoring the state of the instruction cache line that contains code that is executed in the initialisation of the for loop. In practice, this can be achieved with the FLUSH+RELOAD side channel applied on a line of the instruction cache that is executed once per window before the start of the loop. The probe reveals when such a cache line is executed, and the time between two probes would depend on the execution time of the loop. Crucially, the latter depends on j and c0 for each iteration, which would thus be leaked. This strategy is applicable in the case of the _gcry_mpi_powm function: the implementation inlines the logic to determine the the values of j and c0 (and e0) before each iteration of the loop, and so that code fills more than one cache line; the invocation of the multiplication in the inner loop makes one iteration sufficiently long and constant-time so that inter-probe timings measurably encode the number of iterations of the inner loop.

We prototype an end-to-end attack in the SMT-colocated threat model. The prototype uses two SMT-colocated processes, attacker and victim. The victim process may be triggered by the attacker to perform ElGamal decryption. The attacker process uses L1i FLUSH+RELOAD on the virtual address of the memory-mapped libgcrypt.so shared object that contains the instruction cache line to be monitored. To collect side channel data, the attacker partitions time into N slots using the rdtsc instruction: at the beginning of each slot, the target line is loaded into the cache, and the duration of the load operation is measured; after that, the cache line is flushed and finally the remaining (if any) time of the slot is spent in a busy loop. The attacker thus collects N timing samples for load instructions from the target cache line. We establish a threshold for the target system to determine whether the load is likely to have been served from cache (cache hit). We then collect 10,000 measurements by repeatedly triggering the victim. We keep track of each slot across all runs with a set of per-slot counters, all initialised to zero. For each run, whenever the sample of a slot indicates a hit based on the threshold, we increment the value of the corresponding counter.

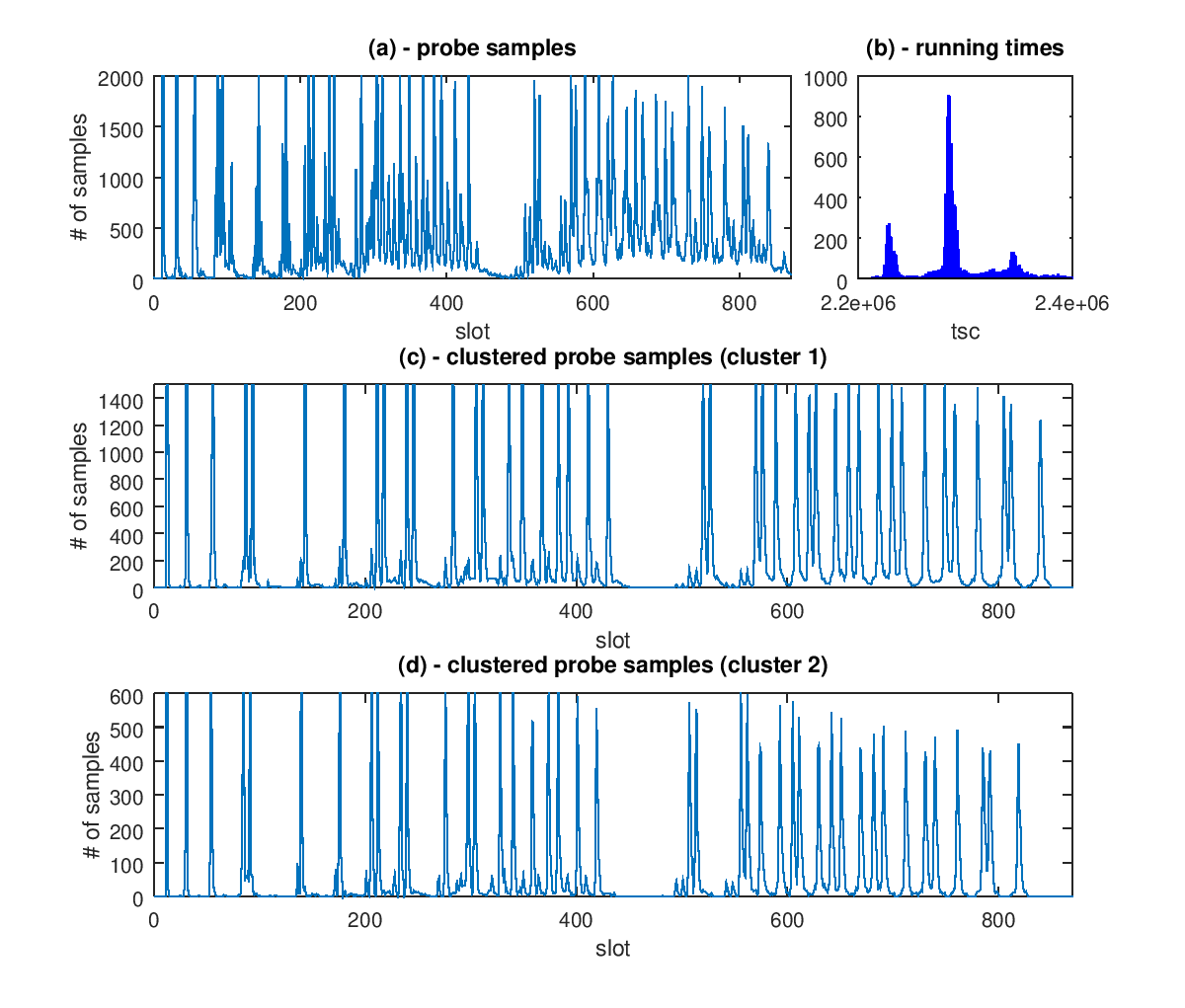
PRIME+PROBE results

Figure 1.a plots the value of the counter of each slot for all runs. While patterns are discernible, the leakage cannot be obtained yet without further data processing. We employ a clustering strategy based on execution time, under the hypothesis that figure 1.a contains samples that are generated at different clock frequencies. Influencing factors are likely to include p-states, c-states, frequency scaling and the power state of certain execution units. Figure 1.b confirms the hypothesis: it plots a histogram of the running times for the whole operation. The distribution of running times has a long tail, but most of the mass is concentrated in the three visible peaks. We use this information to cluster samples and show the results of the clustering in figure 1.c and figure 1.d, showing probes whose running time falls in the interval covered by the highest, and second highest peak, respectively. The peak intervals in the two latter figures accurately encode the leakage for the key used in the exponentiation. The two figures are identical modulo a scaling factor which depends on the difference in running time.

It is interesting to notice that the first few peaks are well synchronised, presumably because the difference in execution time are still within the range of a probing time slot and so they cannot be distinguished by the probes. This presents a very useful tool for the attacker to relax the synchronisation assumptions by constantly monitoring for activity on the target address and start measuring at the first sign of activity.

Exploiting the leakage #

After having obtained the leakage, there is still some work left to do to recover the secret exponent. Recall that the leakage gives us (as highlighted in red in the figure above):

We are thus left with the task of finding the unkwnow bits within the windows themselves. As a warm up, note that when W = 1 there is nothing left to do, as each window consists of exactly one bit, and this is always set to 1. It is clear that the larger the window size W, the more work we expect to do.

We do nothing really special to recover the unknown bits, we’re just a tad smarter than exhaustive search. The Baby-step/giant-step algorithm (see part I of this post) can indeed be adapted to search through a space of n unknown bits for a cost of 2n/2 group operations, regardless of how the unknown bits are distributed.1

The real work is to understand how many unknown bits are left, on average, after the leakage. Mathematics help us here, as it turns out there is an elegant, yet accurate, modeling of the leakage. The details are beyond the scope of this post, but we invite the reader to look into the research paper for more. Here we’ll just note that the leakage approaches a normal distribution, of parameters depending on the window size and on the length of the exponent. The figure below shows the distribution, over 2¹⁴ random exponents, of the number of unknown bits, as the window size W and the exponent length n vary.

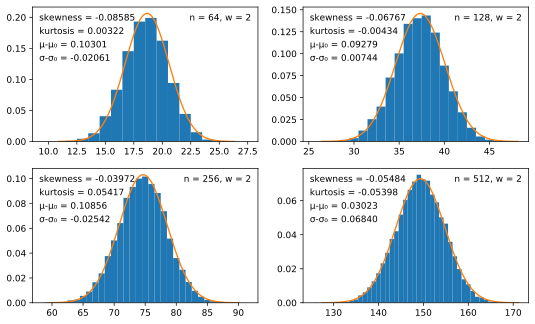
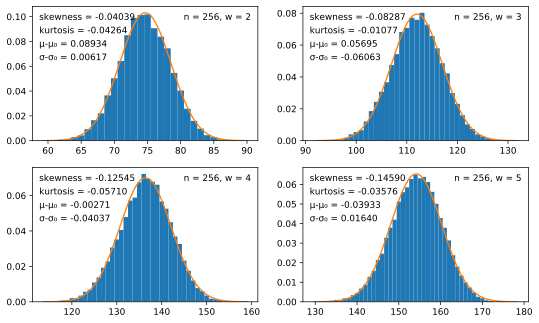
What these graphs show is that some secrets are more at risk than others. First, in each of the graphs above it is apparent that the distribution has a relatively large variance, and thus some secrets will be considerably weaker than the average secret.

Second, and most importantly, cross-implementation scenarios make the vulnerability worse.

In our research we focus on the following scenario:

While some may object that this scenario is unlikely, this is exactly the purpose of having an interoperable standard such as OpenPGP. Why is this scenario better for an attacker? Compare the bit length of secret keys, for, e.g., a prime modulus of 2048 bits:

The difference is remarkable: in the first case, the average number of unknown bits is 180.6, in the second case only 98.0. While in both cases this is below the target security for a 2048 bits modulus, finding the unknown bits in the Libgcrypt case still seems to be infeasible. For Crypto++, on the other hand, an attack requiring 2⁴⁸ group operations seems within reach of a nation state adversary. Worse still, combining the cross-implementation scenario with the effects of the large variance, we estimate that one in 10,000 Crypto++ keys can be recovered for a cost of a few hundred thousand dollars. More modestly, we verified the attack on a much rarer secret key: the weakest among 2²⁸ keys we generated with Crypto++. After obtaining the leakage, our parallel baby-step/giant-step implementation was able to recover the full secret in 30 minutes on 20 cores.

FAQ #

What kind of vulnerability did you find? #

We discovered a side-channel attack against Libgcrypt, which is the library used by the popular GPG suite.

What is the attack scenario? #

A co-located adversary (that is, a malicious user on a shared server, or a malicious VM user on a multi-tenant hosting solution) may be able to recover the secret key used by a victim in the course of decryption of a ciphertext encrypted against an ElGamal key.

Is the attack practical? #

The complexity of the attack entirely depends on the (random) choice of key. Certain keys are weaker than others (and so they can be broken in half an hour, as we have shown), others can only be broken by state actors with large computing power available, while still others are outright unbreakable (because of this specific vulnerability).

Am I affected? #

If you are a GPG (Libgcrypt) user and perform decryption using an ElGamal key, you may be at risk. Update to the latest version of the software. (An additional requirement for the attack is that the adversary be able to run code on your machine).

Endnotes #

  1. Adapting to any pattern of unknown bits is a great feature of Baby-step/giant-step and a few other algorithms, that is unfortunately not shared by other well known discrete logarithm algorithms, such as Pollard’s Rho. ↩

Cite this article