FHE overview#
Protecting data confidentiality happens in three main locations.
At rest, e.g., by using symmetric encryption such as AES-GCM or AES-XTS.
In transit, e.g., by using cryptographic protocols such as TLS 1.3.
In use, e.g., by using Fully Homomorphic Encryption (FHE).
This page provides a short overview of how FHE assists in protecting data confidentiality while in use.
Consider the following simple scenario with two parties a data owner and an untrusted server,
where the data owner wishes to use the server to perform some computations over its data 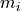 ,
, 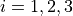 .
.
To accomplish this, the data owner securely transmits the data 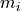 to the server,
possibly employing a secure channel like TLS 1.3.
The server can then evaluate various mathematical operations on this data. Upon completion,
the server ships the results
to the server,
possibly employing a secure channel like TLS 1.3.
The server can then evaluate various mathematical operations on this data. Upon completion,
the server ships the results 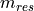 back to the data owner.
back to the data owner.
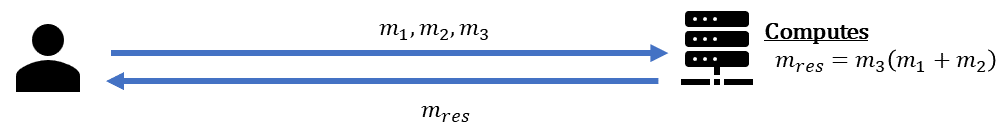
The challenge lies in the fact that the untrusted server can potentially gain access to the confidential information 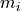 .
To address this concern, the data owner may consider employing a conventional encryption method like AES to encrypt the data,
resulting in ciphertexts
.
To address this concern, the data owner may consider employing a conventional encryption method like AES to encrypt the data,
resulting in ciphertexts 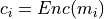 . However, this approach restricts the server from conducting any computations
on the data, essentially reducing it to a mere storage server. This limitation undermines the primary purpose of utilizing the server in the first place.
. However, this approach restricts the server from conducting any computations
on the data, essentially reducing it to a mere storage server. This limitation undermines the primary purpose of utilizing the server in the first place.
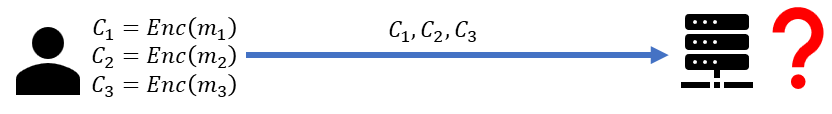
That is precisely where HE can provide assistance. HE empowers the data owner to carry out computations on encrypted data.
By utilizing HE, the data owner can encrypt its confidential data 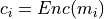 , and upload it to the untrusted server.
The server can then perform operations such as multiplication and addition on the ciphertexts
, and upload it to the untrusted server.
The server can then perform operations such as multiplication and addition on the ciphertexts 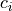 ,
without gaining any knowledge about the original data
,
without gaining any knowledge about the original data 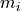 . Upon decrypting the result, the data owner
should obtain an output equivalent to what would have been obtained if the computations were performed on
unencrypted data (within a certain margin of error tolerance).
. Upon decrypting the result, the data owner
should obtain an output equivalent to what would have been obtained if the computations were performed on
unencrypted data (within a certain margin of error tolerance).
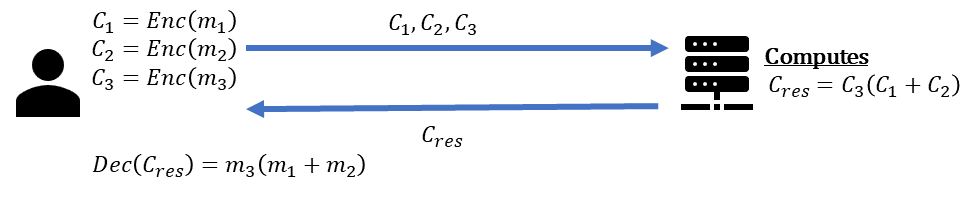
Using additions and multiplications is enough for performing many types of operations in an untrusted environment. For example, performing deep neural network inference operations.
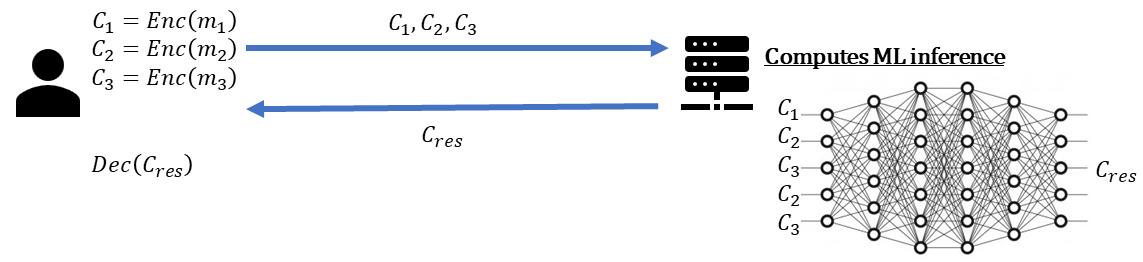
To learn more about the FHE technology see the FHE FAQ section below.
FHE FAQ#
What does a scheme mean in FHE?
An FHE cryptographic scheme is a specific set of algorithms that describe the underlying mathematics being used to perform homomorphic calculations. Different schemes provide different capabilities and have different characteristics.
What capabilities modern FHE schemes provide
Exact FHE schemes such as BGV, B/FV, and TFHE provide at least the following set of operations:
Encryption
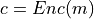 - that receives a data message
- that receives a data message 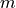 and encrypts it to a ciphertext
and encrypts it to a ciphertext  .
.Decryption
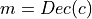 - that receives a ciphertext
- that receives a ciphertext  and decrypt it to the underlying data message
and decrypt it to the underlying data message 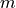 .
.Addition
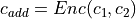 - that receives two ciphertext
- that receives two ciphertext 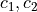 and add them such that
and add them such that 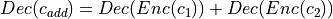 .
.Multiplication
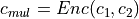 - that receives two ciphertext
- that receives two ciphertext 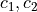 and multiply them such that
and multiply them such that 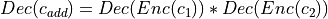 .
.
Approximated FHE schemes such as CKKS provide at least the following set of operations for some small  :
:
Encryption
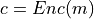 - that receives a data message
- that receives a data message 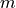 and encrypts it to a ciphertext
and encrypts it to a ciphertext  .
.Decryption
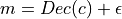 - that receives a ciphertext
- that receives a ciphertext  and decrypt it to the underlying data message
and decrypt it to the underlying data message 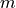 .
.Addition
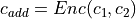 - that receives two ciphertext
- that receives two ciphertext 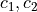 and add them such that
and add them such that 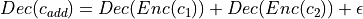 .
.Multiplication
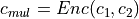 - that receives two ciphertext
- that receives two ciphertext 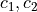 and multiply them such that
and multiply them such that 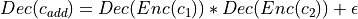 .
.
What FHE schemes exist and why would I use one over the other?
There exist various cryptographic schemes, including BGV, B/FV, TFHE, and CKKS, each with distinct characteristics regarding the input they accept and the output they produce. For instance, BGV, B/FV, and TFHE are designed to operate on integers, enabling operations like database lookups and comparisons of numbers. On the other hand, CKKS is particularly well-suited for handling real or complex numbers, making it suitable for applications such as AI and ML, including tasks like NN inference.
Is FHE quantum-safe and what does quantum-safe mean?
Yes, modern FHE is considered to be quantum-safe. Quantum-safe encryption algorithm maintains the confidentiality of encrypted data even in the presence of large quantum computers. Most FHE schemes today rely on lattice-based cryptography, which is considered secure against quantum attacks.
How is FHE different from a Trusted Execution Environment (TEE)?
With a TEE, one can run computations on unencrypted data with a hardware enforced root of trust. A TEE is intended to be secure by design, however if an application running within it had a security issue (insecure code, application code deployed with malicious malware, zero day exploit, etc), your data may be exposed and an attacker might be able to exfiltrate or manipulate your data.
But with FHE, data remains encrypted at all times even during data leakage or exfiltration. FHE (which guarantees data confidentiality at all times) and a TEE (which provides data integrity) can be combined to secure your ‘crown jewel’ sensitive data. See for example the paper Achieving trustworthy Homomorphic Encryption by combining it with a Trusted Execution Environment.
What are low level primitives?
Low level primitives are the base operations that can be performed directly on ciphertext and include multiplication, addition, and rotation. All higher level functions are implemented in terms of low level primitives, which make them homomorphic as well.
In HElayers, lower level primitives are exposed in its lower level HEbase.
What are high level primitives?
Complex operations like operations on matrices or arrays are built upon the low level primitives. These operations, e.g., tile tensors, are already implemented and provided by HElayers. See relevant APIs in tile tensor.
Is FHE Turing-complete?
FHE is Turing-complete because, in theory, it can perform any function that is computable. Even approximate schemes that until recently were not considered Turing-complete schemes are now such, see BLEACH.
What is the difference between HE, LHE, FHE and PHE?
Partially Homomorphic Encryption (PHE): Refers to schemes that allow performing only one operation on ciphertexts, either addition or multiplication such as Paillier and El-Gamal. PHE schemes are limited in their computational capabilities.
Fully Homomorphic Encryption (FHE): Historically, FHE denoted schemes that could perform both addition and multiplication operations on ciphertexts, making them Turing-complete. FHE schemes offer more flexibility and computational power compared to PHE schemes. Modern schemes such as BGV, B/FV, TFHE and CKKS are FHE schemes.
Levelled Homomorphic Encryption (LHE): In modern schemes, there is a distinction between LHE and FHE. While modern schemes typically incorporate an efficient bootstrap operation, which is considerably slower than other HE operations, there are cases where avoiding bootstrap is beneficial. In LHE, users define the depth of computations in terms of the number of serial multiplications, also known as the level of the evaluated function. LHE has a finite depth limitation, unlike FHE schemes.
HElayers Terminology: HElayers employs the terms HE and FHE interchangeably.