Tile tensors#
Tile tensor is a powerful and simple tool for handling tensors under encryption. It takes care of the packing details, how a tensor is flattened, and how its data is laid out within ciphertexts, while offering the usual API of a tensor, with operations like add, multiply, sum-over-dim, etc.
The packing method is controlled by the tile tensor shape. This is a simple language that defines the shape of the tensor, and how it is packed.
The various options achievable with tile tensor shapes cover many packing options known in the literature (see examples below), unify them to a generic framework, generalize upon them, and add novel possibilities
Tile tensor shapes#
Tile tensor is a tensor divided into tiles, where each tile contains a part of the original tensor, and is stored flattened in a ciphertext.
The tile tensor shape defines the shape of the tensor, and how it is divided
into tiles. For example, the tile tensor shape ![[\frac{5}{2},\frac{6}{4}]](../_images/math/4c1cfb3f4f6b937e772d0c249a87d406c6fc061b.png) specifies the following:
specifies the following:
The numbers above the fraction line indicate the shape of the tensor,
![[5,6]](../_images/math/86ebfe08bed52f8fcdc124d817b7b3403a0b6c78.png) . This means the tile tensor contains a 5 by 6 matrix.
. This means the tile tensor contains a 5 by 6 matrix.The numbers below the line indicate the shape of the tiles,
![[2,4]](../_images/math/9ee224c659df6c62135b7582be9a16a25d3bc560.png) . This means we divided our matrix into contiguous blocks of shape
. This means we divided our matrix into contiguous blocks of shape ![[2,4]](../_images/math/9ee224c659df6c62135b7582be9a16a25d3bc560.png) and stored each such block in a separate ciphertext. This also implies each ciphertext has $8$ slots.
and stored each such block in a separate ciphertext. This also implies each ciphertext has $8$ slots.
See this example in the interactive demo below, where you can try various other shapes, including the options of duplication, unknowns, and interleaved packing.
Demo
Try the following tile tensor shapes:
[5/2,6/4]
[5/2,1/4]
[5/2,*/4]
[5/2,1?/4]
[5/2,6?/4]
[5/2,6~/4]
[5/2,6~?/4]
Logical representation#
A tile tensor 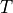 contains some tensor
contains some tensor 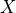 packed divided among several
tiles or ciphertexts.
packed divided among several
tiles or ciphertexts. 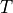 logically represents
logically represents 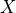 , meaning you can work with
, meaning you can work with 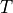 as if it was
as if it was 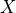 , ignoring the packing details.
, ignoring the packing details.
For example: executing  will return a tile tensor
will return a tile tensor 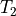 that logically represents a tensor equal to
that logically represents a tensor equal to 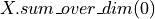 .
.
To simplify working with tile tensors, they provide the same set of operators ordinarily supported by tensors: elementwise operators, matrix-multiplication, sum_over_dim, convolution, rotate (roll), slice, etc.
Here too, the way these operators are implemented covers and generalizes upon many known techniques from the literature. See examples below.
Examples from the literature#
To implement a matrix-vector multiplication of a matrix 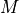 with a vector
with a vector 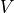 as in [1]. Simply do:
as in [1]. Simply do:
Pack the matrix
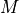 of shape
of shape ![[a,b]](../_images/math/b17897287b23d96473a85f41eeb859a16830b679.png) in a tile tensor
in a tile tensor 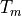 with shape
with shape ![[\frac{a}{t_0},\frac{b}{t_1}]](../_images/math/a48166228f5c7e03e911573c3f4d80d826f50f33.png)
Pack the vector
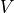 of shape
of shape ![[b]](../_images/math/4af3f9bd3d7d58d9f03b2918edb3ef5119529bb5.png) in a tile tensor
in a tile tensor 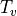 with shape
with shape ![[\frac{*}{t_0},\frac{b}{t_1}]](../_images/math/84cd7c2beb45780ce33e42530a1e353da877780a.png)
Compute the elementwise product
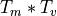 then sum over the second dimension.
then sum over the second dimension.
Here, 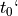 and
and 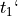 can have any value such that
can have any value such that 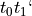 is the number of slots in a given ciphertext.
They can be tuned to optimize various goals, e.g., latency, throughput, memory, or network bandwidth.
is the number of slots in a given ciphertext.
They can be tuned to optimize various goals, e.g., latency, throughput, memory, or network bandwidth.
A generalization for matrix-matrix multiplication as in [2] is as follows.
Pack matrix
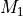 of shape
of shape ![[a,b]](../_images/math/b17897287b23d96473a85f41eeb859a16830b679.png) in a tile tensor
in a tile tensor 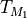 with shape
with shape ![[\frac{a}{t_0},\frac{b}{t_1},\frac{*}{t_2}]](../_images/math/0aa27dd064aeb8659633ea4460e7dfed741bbace.png)
Pack matrix
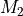 of shape
of shape ![[b,c]](../_images/math/0aa62aa2951d53ef8e953d265724461012c9d0f4.png) in a tile tensor
in a tile tensor 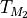 with shape
with shape ![[\frac{*}{t_0},\frac{b}{t_1},\frac{c}{t_2}]](../_images/math/a198573893344d18b5f93c080bde6f73fc76eff1.png)
Compute the elementwise product
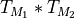 then sum over the second dimension.
then sum over the second dimension.
The authors of HyPHEN [3] describe several methods for convolutional networks that can also be written using the tile tensor notation. For example, the CAConv with SISO method is implemented as follows.
The input image
![[c_i,w_i,h_i]](../_images/math/d91076411f4835bcdf71a960ab3786cfd9cacc43.png) is packed as
is packed as ![[\frac{c_i}{2},\frac{w_i}{32},\frac{h_i}{32}]](../_images/math/38631d0973e5cc6f676812804904fc00b7108839.png) .
.The kernels
![[c_o,c_i,f_w,f_h]](../_images/math/cf6896c91b3c5d9acb5d276e7cce8056513cddd7.png) are packed as
are packed as ![[f_w,f_h,\frac{c_i}{2},c_o,\frac{*}{32},\frac{*}{32}]](../_images/math/ec5467d9943ef5e44a2e7faa1a974c8c8aa9bcbd.png) .
.The computation is the same as the tile tensor’s convolution operator.
The result is packed as
![[\frac{*}{2},c_o,\frac{w_i}{32},\frac{h_i}{32}]](../_images/math/adb5fa00f0c2cd26165dbe704475e3a17106427f.png) .
.
Tile tensors generalize on the above, using interleaved packing to support arbitrary image size and arbitrary tile sizes.
References#
[1] Crockett, E.: A low-depth homomorphic circuit for logistic regression model training. Cryptology ePrint Archive (2020). Link
[2] Rizomiliotis, P., Triakosia, A.: On matrix multiplication with homomorphic encryption. In: Proceedings of the 2022 on Cloud Computing Security Workshop, CCSW’22, p. 53–61. Association for Computing Machinery, New York, NY, USA (2022). Link
[3] Kim, D., Park, J., Kim, J., Kim, S., Ahn, J.H.: HyPHEN: A hybrid packing method and its optimizations for homomorphic encryption-based neural networks. IEEE Access (2023) Link.
[4] KKrastev, A., Samardzic, N., Langowski, S., Devadas, S., & Sanchez, D. (2024). A Tensor Compiler with Automatic Data Packing for Simple and Efficient Fully Homomorphic Encryption. Proceedings of the ACM on Programming Languages, 8(PLDI), 126-150. Link.
 and
and 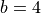 is reshaped to
is reshaped to ![[2,2,2, 2,2]](../_images/math/9782d900c275866d21067aa6dbb0a0293f8fff45.png) ,
where the first three dimensions come from the ‘a’ dimension and are labeled a0,a1,a2,
and the last two come from the ‘b’ dimension and are labeled b0,b1.
,
where the first three dimensions come from the ‘a’ dimension and are labeled a0,a1,a2,
and the last two come from the ‘b’ dimension and are labeled b0,b1.![[2,2,2]](../_images/math/5141b909cea7475efc352b012ed1235221552506.png) in our example. The tensor
can now be packed in various ways, e.g.
in our example. The tensor
can now be packed in various ways, e.g. ![[a0,a1,a2/2,b0/2,b1/2]](../_images/math/d9d28c37ce12eb69d2d65d1fa1d7749f0ede7e72.png) or
or ![[b0,b1,a0/2,a1/2/a2/2]](../_images/math/4a3d0ef4d121546e51ea08b90be9915852810fdc.png) . In Fhelipe’s notation,
the same thing is written
. In Fhelipe’s notation,
the same thing is written ![[a0,a1;a2,b0,b1]](../_images/math/5506019c0aea0cbd7999b7273eeda5bc55002e47.png) or
or ![[b0,b1;a0,a1,a2]](../_images/math/02a81bd64923266da49f91c94cf9b4649b2aab3b.png) .
.![[2,2,...2]](../_images/math/82cc55e731679848bcb6a2da92e3d6d70693a618.png) . In the above example, if the tensor’s original shape is
. In the above example, if the tensor’s original shape is ![[80,4]](../_images/math/600a55a2eb0d4f34eeb9d66535491e7d15d8dd50.png) , Fhelipe would require first padding it to a larger size of
, Fhelipe would require first padding it to a larger size of ![[128,4]](../_images/math/6348d54439f6cc97fb2cd90e4dbcadb4fd9fe58e.png) , to enable breaking down both dimensions to size-2 dimensions. This causes a considerable waste.Using tile tensors, working with a tile tensor shape of
, to enable breaking down both dimensions to size-2 dimensions. This causes a considerable waste.Using tile tensors, working with a tile tensor shape of ![[80/4,4/2]](../_images/math/cea7414f46f44d778503c76f240ee394c04f893d.png) or
or ![[80/2,4/4]](../_images/math/b09289f140071c5b9ae54b3b23895421506a5634.png) would provide maximal efficiency in terms of both storage and computation time.
would provide maximal efficiency in terms of both storage and computation time.