Logical Neural Networks

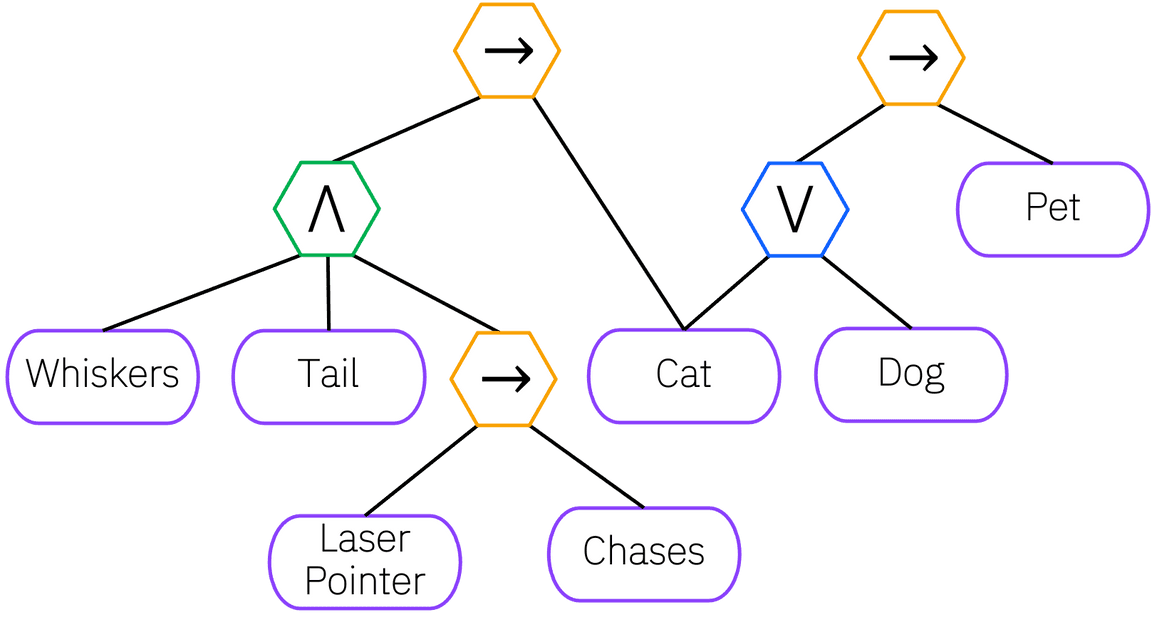
LNNs are a novel Neuro = Symbolic framework designed to seamlessly provide key properties of both neural nets (learning) and symbolic logic (knowledge and reasoning).

Every neuron has a meaning as a component of a formula in a weighted real-valued logic, yielding a highly interpretable disentangled representation.
Inference is omnidirectional, which corresponds to logical reasoning and includes classical first-order logic (FOL) theorem proving with quantifiers.
Intermediate neurons are inspectable and may individually specify targets and error signals, rather than focussing on predefined target variables at the last layer of the network.
The model is end-to-end differentiable, and learning minimizes a novel loss function capturing logical contradiction, yielding resilience to inconsistent knowledge.
Bounds on truths (as ranges) enable the open-world assumption, which can have probabilistic semantics and offer resilience to incomplete knowledge.

Example of Logical Neural Network — LNN - An Interpretable Neural Reasoner

Quickstart

To install the LNN:

Install GraphViz

Run:

pip install git+https://github.com/IBM/LNN.git

Documentation

Read the Docs	Academic Papers	Educational Resources	Neuro-Symbolic AI	API Overview	Python Module

Citation

If you use Logical Neural Networks for research, please consider citing the reference paper:

@article{riegel2020logical,
  title={Logical neural networks},
  author={Riegel, Ryan and Gray, Alexander and Luus, Francois and Khan, Naweed and Makondo, Ndivhuwo and Akhalwaya, Ismail Yunus and Qian, Haifeng and Fagin, Ronald and Barahona, Francisco and Sharma, Udit and others},
  journal={arXiv preprint arXiv:2006.13155},
  year={2020}
}

Main Contributors

Naweed Khan, Ndivhuwo Makondo, Francois Luus, Dheeraj Sreedhar, Ismail Akhalwaya, Richard Young, Toby Kurien

Edit this page on GitHub

FOL-LNN

Logical Neural Networks

Quickstart

Documentation

Citation

Main Contributors