LNN Module

Symbolic Structure

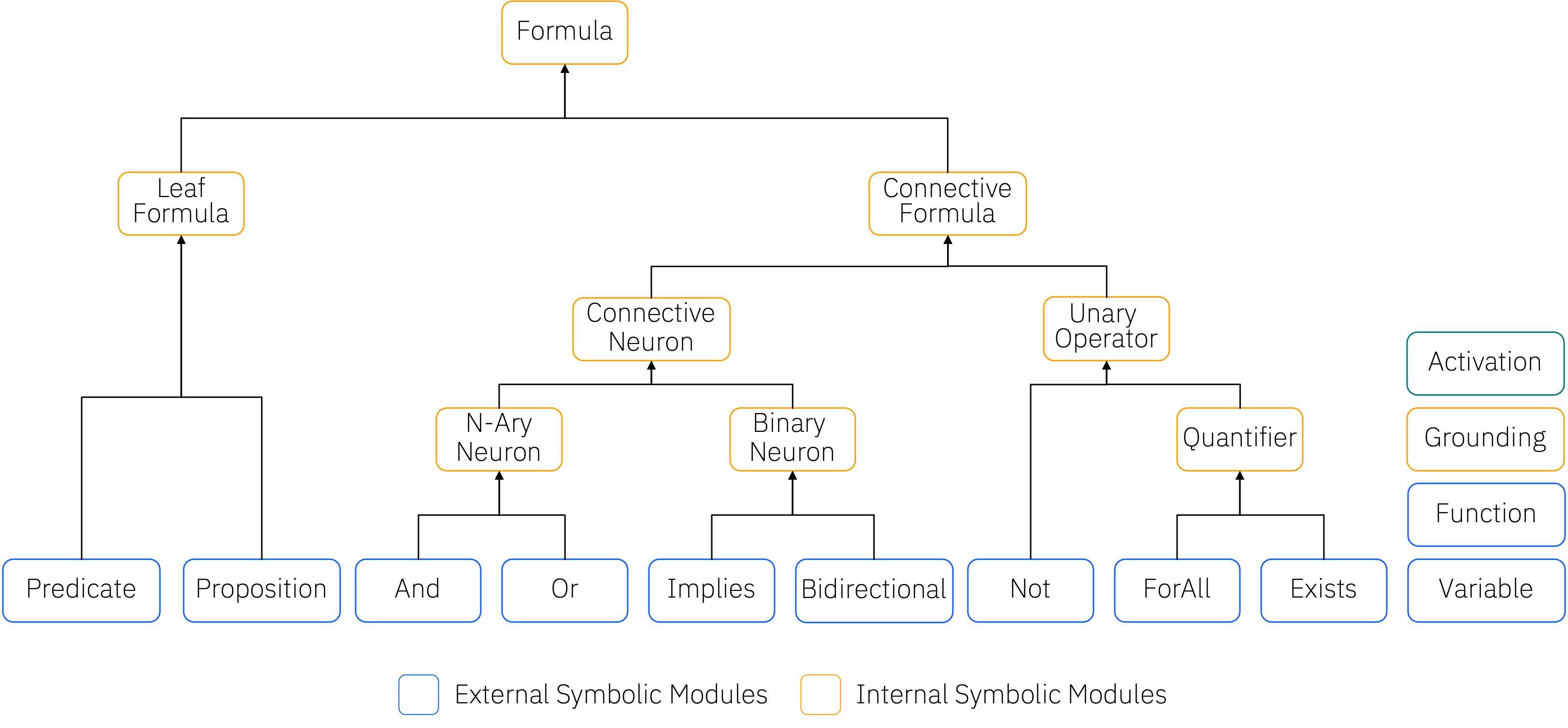
Symbolic Modules

class lnn. And ( * formula : Formula , ** kwds )

Symbolic n-ary conjunction .

Returns a logical conjunction where inputs can be propositions , called first-order logic predicates or any other connective formulae . Propositional inputs yield a propositional node, whereas if any input is a predicate it will cause the connective to increase its dimension to also be a FOL node (i.e. stores a table of facts).

Parameters :

• *formula ( Formula ) – A variable length argument list that accepts any number of input formulae objects as arguments.

• name ( str , optional ) – A custom name for the node to be used for identification and custom printing. If unspecified, defaults the structure of the node.

• activation ( dict , optional ) – Parameters given as a dictionary of configuration options, see the neural configuration for more details

Examples

# Propositional
A, B, C = Propositions('A', 'B', 'C')
And(A, B, C)

# First-order logic
x, y = Variables('x', 'y')
A, C = Predicates('A', 'C')
B = Predicate('B', arity=2)
And(A(x), B(x, y), C(y)))

class lnn. Congruent ( * formulae : Formula , ** kwds )

Symbolic Congruency

This is used to define nodes that are symbolically equivalent to one another (despite the possibility of neural differences)

add_data ( facts : Union [ Fact , Tuple , Set , Dict ] )

Should not be called by the user

downward ( index : Optional [ int ] = None , groundings : Optional [ Set [ Union [ str , Tuple [ str , ... ] ] ] ] = None , ** kwds ) → Optional [ Tensor ]

Downward inference from the operator to the operands.

Parameters :

• index ( int , optional ) – restricts downward inference to an operand at the specified index. If unspecified, all operands are updated.

• groundings ( str or tuple of str , optional ) – restrict upward inference to a specific grounding or row in the truth table

Returns :

tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step.

Return type :

float

class lnn. Direction ( value )

An enumeration for the direction of inference.

Used to restrict an inference pass (of a particular node or the entire model) to a single pass of the specified direction.

Parameters :

• DOWNWARD – Evaluation of operands given the operator and the rest of the operands

• UPWARD – Evaluation of the operator given the operands

class lnn. Exists ( * args , ** kwds )

Symbolic existential quantifier.

When working with belief bounds - existential operators restrict upward inference to only work with the given formula’s lower bound. Downward inference behaves as usual.

Parameters :

• *variables ( Variable ) –

• formula ( Formula ) – The FOL formula to quantify over, may be a connective formula or a Predicate.

Examples

No free variables, quantifies over all of the variables in the formula.

Some_1 = Exists(birthdate(p, d)))
Some_2 = Exists(p, d, birthdate(p, d)))

Free variables, quantifies over a subset of variables in the formula.

Some = Exists(p, birthdate(p, d)))

Warning

Quantifier with free variables, not yet implemented. It is required that we quantify over all the variables given in the formula, either by specifying all the variables or but not specifying any variables - which is equivalent to quantifying over all variables.

class lnn. Fact ( value )

An enumeration for facts.

Parameters :

• CONTRADICTION – A classical interpretation of a contradictory input. Contradictions arise by disagreement of two signal, most often coming from different directions (UPWARD+DOWNWARD). This can be interpreted as a disagreement between the data and the logic, or more appropriately - introducing data to a logic that violates soundness and thereby moves the model into worlds that are not consistent with the logic.

• FALSE – Classically False inputs as represented by LNN bounds

• TRUE – Classically True inputs as represented by LNN bounds

• UNKNOWN – A classical interpretation of what would be an unknown input, this is represented by LNN bounds with complete uncertainty

class lnn. Forall ( * args , ** kwds )

Symbolic universal quantifier.

When working with belief bounds - universal operators restrict upward inference to only work with the given formula’s upper bound. Downward inference behaves as usual.

Parameters :

• *variables ( Variable ) –

• formula ( Formula ) – The FOL formula to quantify over, may be a connective formula or a Predicate.

Examples

No free variables, quantifies over all of the variables in the formula.

All_1 = Forall(birthdate(p, d)))
All_2 = Forall(p, d, birthdate(p, d)))

Free variables, quantifies over a subset of variables in the formula.

All = Forall(p, birthdate(p, d)))

Warning

Quantifier with free variables, not yet implemented. It is required that we quantify over all the variables given in the formula, either by specifying all the variables or but not specifying any variables - which is equivalent to quantifying over all variables.

class lnn. Formula ( * formulae : Formula , name : Optional [ str ] = '' , arity : Optional [ int ] = None , ** kwds )

Symbolic container for a generic formula.

add_data ( data : Union [ bool , Fact , float , Tuple [ float , float ] , Dict [ Union [ str , Tuple [ str , ... ] ] , Union [ bool , Fact , float , Tuple [ float , float ] ] ] ] )

Add data to the formula in the form of classical facts or belief bounds.

Data given is a Fact or belief bounds assumes a propositional formula. Data given in a dict assumes a first-order logic formula, keyed by the grounding and a value given as a Fact or belief bounds.

Parameters :

data ( Fact , belief bounds or dict ) – For propositional formulae, truths is given as either Facts or belief bounds. These beliefs can be given as a bool, float or a float-range, i.e. a tuple of 2 floats. For first-order logic formula, inputs truths are given as a dict. It is keyed by the grounding (a str for unary formlae or tuple of strings of larger arities), with values also as Facts or bounds on beliefs.

Examples

# propositional
P, Q = Propositions("P", "Q")
P.add_data(Fact.TRUE)
Q.add_data((.1, .4))

# first-order logic
Person = Predicate("Person")
Person.add_data({
    "Barack Obama": Fact.TRUE,
    "Bo": (.1, .4)
})

# FOL with arity > 2
BD = Predicate("Birthdate", 2)
BD.add_data({
    ("Barack Obama", "04 August 1961"): Fact.TRUE,
    ("Bo", "09 October 2008"): (.6, .75)
})

add_labels ( labels : Union [ Fact , Tuple [ float , float ] , Dict [ Union [ str , Tuple [ str , ... ] ] , Union [ Fact , Tuple [ float , float ] ] ] ] )

Store labels as data within the symbolic container.

Labels given is a Fact or belief bounds assumes a propositional formula. Labels given in a dict assumes a first-order logic formula, keyed by the grounding and a value given as a Fact or belief bounds.

Parameters :

labels ( Fact , belief bounds or dict ) – For propositional formulae, facts are given as either Facts or bounds on beliefs (a tuple of 2 floats). For first-order logic formula, inputs are given as a dict. It is keyed by the grounding (a str for unary formlae or tuple of strings of larger arities), with values also as Facts or bounds on beliefs.

Examples

# propositional
P, Q = Propositions("P", "Q")
P.add_labels(Fact.TRUE)
Q.add_labels((.1, .4))

# first-order logic
Person = Predicate("Person")
Person.add_labels({
    "Barack Obama": Fact.TRUE,
    "Bo": (.1, .4)
})

# FOL with arity > 2
BD = Predicate("Birthdate", 2)
BD.add_labels({
    ("Barack Obama", "04 August 1961"): Fact.TRUE,
    ("Bo", "09 October 2008"): (.6, .75)
})

contradicting_bounds ( bounds : Optional [ Tensor ] = None , stacked = False ) → BoolTensor

Check which bounds are in contradiction.

contradicting_stacked_bounds ( bounds : Optional [ Tensor ] = None ) → BoolTensor

Check if bounds are in contradiction.

flush ( )

Set all facts in formula to Fact.UNKNOWN .

get_data ( * groundings : Union [ str , Tuple [ str , ... ] , tuple [ str ] ] ) → Tensor

Returns the current beliefs of the formula.

Uses the given groundings or the entire groundind_table to slice out the current belief bounds from the bounds_table .

Parameters :

*groundings ( str or tuple of str ) – NB - if unspecified, defaults to returning all the facts for the given formula. If specified, the table will be ordered according to the input grounding order.

get_labels ( * groundings : str ) → Tensor

Returns the stored labels from the symbolic container.

property groundings : Set [ Union [ str , Tuple [ str , ... ] ] ]

Returns the groundings to the user as str or tuple of str.

property is_classically_resolved

Checks if the query node is in a classical state besides Fact.UNKNOWN .

is_contradiction ( bounds : Optional [ Tensor ] = None , stacked = False ) → BoolTensor

Check if there are any bounds in contradiction.

is_equal ( other : Formula ) → bool

Returns True if two nodes are symbolically equivalent.

Formulae can be symbolically equivalent yet neurally different, example:

f = And(A, B, activation={"type": NeuralActivation.Lukasiewicz})
g = And(A, B, activation={"type": NeuralActivation.Godel})

The above will return True , since f is symbolically equivalent to g despite different neural configurations.

print ( header_len : int = 50 , roundoff : int = 5 , params : bool = False , grads : bool = False , numbering : bool = False )

Print the states of groundings in a formula.

OPEN   Proposition: A                 UNKNOWN (L, U)

CLOSED Proposition: B                   FALSE (L, U)

OPEN   Predicate: P1 (x)
"const_1"                                TRUE (L, U)
"const_2"                       CONTRADICTION (L, U)
"const_3"                               FALSE (L, U)

OPEN   Predicate: P2 (x, y)
("const_1", "const_5")                   TRUE (L, U)
("const_2", "const_6")          CONTRADICTION (L, U)
("const_3", "const_7")                  FALSE (L, U)

OPEN   And: And_0 (x, y)
Bindings: P1 (x: "const_1"), P2 (x: 'const_2', y: ['const_3', ...])
('const_1', 'const_3')                   TRUE (L, U)
('const_2', 'const_3')          CONTRADICTION (L, U)
('const_1', 'const_7')                  FALSE (L, U)

TRUE   Forall: Forall_0 (y)           UNKNOWN (L, U)

set_negative_weights ( is_negative : bool = True , store : bool = True )

absorb Not into weights and allow negative computation

set_propositional ( propositional : bool )

Set’s the neuron’s world parameter.

state ( groundings : Optional [ Union [ str , Tuple [ str , ... ] , List [ str ] , List [ Tuple [ str , ... ] ] ] ] = None , to_bool : bool = False , bounds : Optional [ Tensor ] = None ) → Union [ Tensor , Dict [ Union [ str , Tuple [ str , ... ] ] , Tensor ] ]

Returns the state of a single grounded fact.

if to_bool flag is True, will map classical Facts to bool: i.e. {Fact.True: True, FALSE’: False} The rest of the node states will return as str

Notes

see section F.2 for more information on node states

property world : World

Proxy to get the neuron’s world parameter.

world_state ( name = False )

Returns the state of the world variable.

class lnn. Iff ( lhs : Formula , rhs : Formula , ** kwds )

Symbolic Equivalence - a bidirectional binary implication or IFF (if and only if) node.

Returns a logical bidirectional equivalence node where inputs can be ` propositions <LNN.html#lnn.Proposition>`_, called first-order logic predicates or any other connective formulae . Propositional inputs yield a propositional node, whereas if any input is a predicate it will cause the connective to increase its dimension to also be a FOL node (i.e. stores a table of facts).

Parameters :

• lhs ( Formula ) – The left-hand side formula of the binary inputs to the connective.

• rhs ( Formula ) – The right-hand side formula of the binary inputs to the connective.

• name ( str , optional ) – A custom name for the node to be used for identification and custom printing. If unspecified, defaults the structure of the node.

• activation ( dict , optional ) –

  parameters given as a dictionary of configuration options, see the neural configuration for more details

Examples

# Propositional
A, B = Propositions('A', 'B')
Iff(A, B)

# First-order logic
x, y = Variables('x', 'y')
A = Predicate('A')
B = Predicate('B', arity=2)
Iff(A(x), B(x, y)))

downward ( index : Optional [ int ] = None , groundings : Optional [ Set [ Union [ str , Tuple [ str , ... ] ] ] ] = None , ** kwds ) → float

Downward inference from the operator to the operands.

Parameters :

• index ( int , optional ) – restricts downward inference to an operand at the specified index. If unspecified, all operands are updated.

• groundings ( str or tuple of str , optional ) – restrict upward inference to a specific grounding or row in the truth table

Returns :

tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step.

Return type :

float

upward ( groundings : Optional [ Set [ Union [ str , Tuple [ str , ... ] ] ] ] = None , ** kwds ) → float

Upward inference from the operands to the operator.

Parameters :

groundings ( str or tuple of str ) – restrict upward inference to a specific grounding or row in the truth table

Returns :

tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step.

Return type :

float

class lnn. Implies ( lhs : Formula , rhs : Formula , ** kwds )

Symbolic binary implication .

Returns a logical implication node where inputs can be propositions , called first-order logic predicates or any other connective formulae . Propositional inputs yield a propositional node, whereas if any input is a predicate it will cause the connective to increase its dimension to also be a FOL node (i.e. stores a table of facts).

Parameters :

• lhs ( Formula ) – The left-hand side formula of the binary inputs to the connective.

• rhs ( Formula ) – The right-hand side formula of the binary inputs to the connective.

• name ( str , optional ) – A custom name for the node to be used for identification and custom printing. If unspecified, defaults the structure of the node.

• activation ( dict , optional ) –

  Parameters given as a dictionary of configuration options, see the neural configuration for more details

Examples

# Propositional
A, B = Propositions('A', 'B')
Implies(A, B)

# First-order logic
x, y = Variables('x', 'y')
A = Predicate('A')
B = Predicate('B', arity=2)
Implies(A(x), B(x, y)))

class lnn. Loss ( value )

An enumeration for standard loss functions used during training.

Parameters :

• CONTRADICTION – Ensures logical consistency.

• CUSTOM – Not Implemented.

• LOGICAL – Enforces logical constraints.

• SUPERVISED – Targets labels .

• UNCERTAINTY – Reduces the uncertainty of bounds.

class lnn. Model ( knowledge : Optional [ Union [ Formula , Iterable [ Formula ] ] ] = None , data : Optional [ Dict ] = None , name : str = 'Model' )

Creates a container for logical reasoning and neural learning.

Models define a theory or a collection of formulae, with additional reasoning and learning functionality that can be applied to each formula in the model. In contrast to standard FOL where the existence of a formula symbol assumes a True truth value, the data associated with LNN formulae can take on any classical truth (Fact) or belief bounds (a range real-values).

Models are also dynamic, instantiated as empty containers which are later populated with knowledge rules and data. This additionally allows LNNs to operate in dynamic environments whereby the knowledge acquired may grow as new information becomes available.

Parameters :

name ( str , optional ) – Name of contextual model, defaults to “Model”

graph

Directed graph that connects nodes, pointing from operator to operand nodes.

Type :

nx.DiGraph

nodes

Each formula is keyed by a formula_number, with the value as the formula object.

Type :

dict

query

A formula node that is set as the current query - allows the model to be used in QA/theorem proving whereby inference is governed towards solving the query.

Type :

Formula

Examples

# define the predicates
x, y = Variables("x", "y")
Smokes, Asthma, Cough = Predicates("Smokes", "Asthma", "Cough")
Friends = Predicate("Friends", arity=2)

# define the connectives/quantifiers
Smokers_have_friends = And(Smokes(x), Friends(x, y))
Asthmatic_smokers_cough = (
    Exists(x, Implies(And(Smokes(x), Asthma(x)), Cough(x))))
Smokers_befriend_smokers = (
    Forall(x, y, Implies(Smokers_have_friends(x, y), Smokes(y))))

# add root formulae to model
model = Model()
model.add_knowledge(
    Asthmatic_smokers_cough,
    Smokers_befriend_smokers)

# add data to the model
model.add_data({
    Smokes: {
        "Person_1": Fact.TRUE,
        "Person_2": Fact.UNKNOWN,
        "Person_3": Fact.UNKNOWN},
    Friends: {
        ("Person_1", "Person_2"): Fact.TRUE,
        ("Person_2", "Person_3"): Fact.UNKNOWN}})

# reason over the model
model.infer()

# verify the model outputs
model.print()

add_data ( data : Dict [ Formula , Union [ bool , Fact , float , Tuple [ float , float ] , Dict [ Union [ str , Tuple [ str , ... ] ] , Union [ bool , Fact , float , Tuple [ float , float ] ] ] ] ] )

Add data to select formulae in the model, in the form of classical facts or belief bounds.

Data given is a Fact or belief bounds assumes a propositional formula. Data given in a dict assumes a first-order logic formula, keyed by the grounding and a value given as a Fact or belief bounds.

Parameters :

data ( a dict of Fact , belief bounds or dict ) – The dict is keyed by the formula for which data is to be added, with the truths as the value. For propositional formulae, truths are given as either Facts or belief bounds. These beliefs can be given as a bool, float or a float-range, i.e. a tuple of 2 floats. For first-order logic formula, inputs truths are given as a dict. This is further keyed by the grounding (a str for unary formlae or tuple of strings of larger arities), with values also as Facts or bounds on beliefs.

Examples

# propositional
P = Proposition("Person")
model.add_data({
    P: Fact.TRUE
})

# first-order logic
Person = Predicate("Person")
BD = Predicate("Birthdate", 2)
model.add_data({
    Person: {
        "Barack Obama": Fact.TRUE,
        "Bo": (.1, .4)
    },
    BD: {
        ("Barack Obama", "04 August 1961"): Fact.TRUE,
        ("Bo", "09 October 2008"): (.6, .75)
    }
})

Warning

Assumes that the formulae have already been inserted into the model, see add_knowledge for more details.

add_knowledge ( * formulae : Formula , world : Optional [ World ] = None )

Extend the model to include additional formulae.

Only root level formulae explicitly need to be added to the model. Unless otherwise specified, each root formula follows the open world assumption.

Examples

P, Q = Predicates("P1", "Q")
model.add_knowledge(P, Q)

creates the predicate and inserts into the model

or

model = Model()
P1 = Predicate("P1")
P2 = Predicate("P2", 2)
P3 = Predicate("P3", 3)
model.add_knowledge(
    And(P1(x), P2(x, y)),
    Implies(P2(x, y), P3(x, y, z))
)

inserts the formulae roots into the model and appropriately includes all subformulae also into the scope of the model.

Any formulae that directly require inquiry should first be created in the user scope and thereafter inserted into the model for reference after reasoning/learning

e.g.

model = Model()
P1 = Predicate("P1")
P2 = Predicate("P2", 2)
P3 = Predicate("P3", 3)
my_and = And(P1(x), P2(x, y))
model.add_knowledge(
    my_and,
    Implies(P2(x, y), P3(x, y, z))
)

...
model.infer()
...

my_and.state()

add_labels ( labels : Dict [ Formula , Union [ Fact , Tuple [ float , float ] , Dict [ Union [ str , Tuple [ str , ... ] ] , Union [ Fact , Tuple [ float , float ] ] ] ] ] )

Add labels to select formulae in the model, in the form of classical facts or belief bounds.

Labels given is a Fact or belief bounds assumes a propositional formula. Labels given in a dict assumes a first-order logic formula, keyed by the grounding and a value given as a Fact or belief bounds.

Parameters :

labels ( a dict of Fact , belief bounds or dict ) – The dict is keyed by the formula for which data is to be added, with the truths as the value. For propositional formulae, truths are given as either Facts or belief bounds (a tuple of 2 floats). For first-order logic formula, inputs truths are given as a dict. This is further keyed by the grounding (a str for unary formlae or tuple of strings of larger arities), with values also as Facts or bounds on beliefs.

Examples

# propositional
P = Proposition("Person")
model.add_labels({
    P: Fact.TRUE
})

# first-order logic
Person = Predicate("Person")
BD = Predicate("Birthdate", 2)
model.add_labels({
    Person: {
        "Barack Obama": Fact.TRUE,
        "Bo": (.1, .4)
    },
    BD: {
        ("Barack Obama", "04 August 1961"): Fact.TRUE,
        ("Bo", "09 October 2008"): (.6, .75)
    }
})

Warning

Assumes that the formulae have already been inserted into the model, see add_knowledge for more details.

downward ( ** kwds )

Performs downward inference for each node in the model from root to leaf.

infer ( direction : Optional [ Direction ] = None , source : Optional [ Formula ] = None , max_steps : Optional [ int ] = None , ** kwds ) → Tuple [ Tuple [ int , int ] , Tensor ]

Reasons over all possible inferences until convergence

Parameters :

• direction ( {Direction.UPWARD , Direction.DOWNWARD} , optional ) – Can be specified as either UPWARD or DOWNWARD inference, a single pass of that direction will be applied. If unspecified, defaults to the LNN naive inference strategy of doing inference until convergence.

• source ( node , optional ) – Specifies starting node for depth-first search traversal . Specifying a node here will compute reasoning (until convergence) on the subgraph, with the specified source is the root of the subgraph.

• max_steps ( int , optional ) – Limits the inference to a specified number of passes of the naive traversal strategy. If unspecified, the steps will not be limited, i.e. inference will take place until convergence.

Returns :

(steps, facts_inferred)

Return type :

Tuple[tuple of 2 ints, torch.Tensor]

infer_query ( * args , ** kwds ) → Tuple [ Tuple [ int , int ] , Tensor ]

Reasons only over the stored query.

Is the same as calling model.infer but setting the source node as model.query .

named_parameters ( )

Returns an iterator over module parameters, yielding both the name of the parameter as well as the parameter itself.

Parameters :

• prefix ( str ) – prefix to prepend to all parameter names.

• recurse – if True, then yields parameters of this module

and all submodules. Otherwise, yields only parameters that are direct members of this module. :type recurse: bool

Yields :

(str, Parameter) – Tuple containing the name and parameter

Example:

.. code::

>>> # xdoctest: +SKIP("undefined vars")
>>> for name, param in self.named_parameters():
>>>    if name in ['bias']:
>>>        print(param.size())

parameters ( )

Returns an iterator over module parameters.

This is typically passed to an optimizer.

Parameters :

recurse – if True, then yields parameters of this module

and all submodules. Otherwise, yields only parameters that are direct members of this module. :type recurse: bool

Yields :

Parameter – module parameter

Example:

.. code::

>>> # xdoctest: +SKIP("undefined vars")
>>> for param in model.parameters():
>>>     print(type(param), param.size())
<class 'torch.Tensor'> (20L,)
<class 'torch.Tensor'> (20L, 1L, 5L, 5L)

set_query ( formula : Formula , world = World.OPEN , converge = False )

Inserts a query node into the model and maintains a handle on the node.

Parameters :

• formula ( Formula ) – Name of contextual model

• world ( World ) – Default behavior of the formula. If unspecified, assumes open world assumption.

Notes

The query formula will be added to the model and will not be removed, even if a new query is defined using this function.

train ( losses : Union [ Loss , List [ Loss ] , Dict [ List [ Loss ] , float ] ] , ** kwds )

Train the model.

Reasons across the model until convergence using the standard inference strategy - equivalent to running a NN in the forward direction. At the end of each reasoning pass losses are calculated according to a predefined or custom loss and model parameters are updated. An epoch constitutes all computation until parameters take a step.

Parameters :

• losses ( Loss , list or dict of losses ) – Predefined losses expected from the fixed Loss constants. If given in dict form, coefficients of each loss can be specified as a float value. The value can alternatively specify additional parameters for each loss calculation using a dict.

• optimizer ( pytorch optimizer , optional ) – Custom optimizers should be instantiated with the model parameters using model.parameters() . If unspecified, defaults to Adam .

• learning_rate ( float , optional ) – If unspecified, defaults to 5e-2.

• epochs ( float , optional ) – Number of training epochs. If unspecified, trains for 3e2 epochs.

• pbar ( bool , optional ) – Prints out a tqdm training progress bar. If unspecified, does not print out.

Returns :

(epochs, total_loss) – A tuple of variables are returned. The epochs is number of epochs trained before stopped/converged + 1. The total_loss returns a tuple of 2 values: first is the running_loss as a list for the sum of loss at the end of each epoch; then the loss_history , which is a Tensor of individual loss components as specified by the losses argument.

Return type :

Tuple[int, Tuple[List, Tensor]]

Examples

# construct the model from formulae
model = Model()
p1, p2 = Predicates("P1", "P2")
x = Variable("x")
AB = And(p1(x), p2(x))
model.add_knowledge(AB)

# add data to the model
model.add_data({
    p1: {
        "0": Fact.TRUE,
        "1": Fact.TRUE,
        '2': Fact.FALSE,
        '3': Fact.FALSE
    },
    p2: {
        '0': Fact.TRUE,
        '1': Fact.FALSE,
        '2': Fact.TRUE,
        '3': Fact.FALSE,
    }
})

# add supervisory targets
model.add_labels({
    AB: {
        '0': Fact.TRUE,
        '1': Fact.FALSE,
        '2': Fact.TRUE,
        '3': Fact.FALSE,
    }
})

# train the model and output results
model.train(losses=Loss.SUPERVISED)
model.print(params=True)

upward ( ** kwds )

Performs upward inference for each node in the model from leaf to root.

class lnn. NeuralActivation ( value )

An enumeration of t-norms for alternate neural computations.

Used to replace the activation of a connective with the specified activation.

Parameters :

• Frechet – Unweighted Frechet - only implemented for propositional logic.

• Godel – Unweighted Godel - only implemented for propositional logic.

• Lukasiewicz – Weighted Łukasiewicz , supported for full first order logic.

• LukasiewiczTransparent ( default ) – Modification of weighted Łukasiewicz that supports learning by allowing identity gradients through the clamped regions.

• Product – Unweighted Product - only implemented for propositional logic.

class lnn. Not ( formula : Formula , ** kwds )

Symbolic Negation

Returns a logical negation where inputs can be propositional, first-order logic predicates or other connectives.

Parameters :

formula ( Formula ) – accepts a unary input Formula

Examples

# Propositional
A = Proposition('A')
Not(A)

# First-order logic
x, y = Variables('x', 'y')
A = Predicate('A', arity=2)
Not(A(x, y)))

downward ( ** kwds ) → Tensor

Downward inference from the operator to the operands.

Returns :

tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step.

Return type :

float

upward ( ** kwds ) → float

Upward inference from the operands to the operator. :returns: tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step. :rtype: float

class lnn. Or ( * formula , ** kwds )

Symbolic n-ary disjunction .

Returns a logical disjunction where inputs can be propositions , called first-order logic predicates or any other connective formulae . Propositional inputs yield a propositional node, whereas if any input is a predicate it will cause the connective to increase its dimension to also be a FOL node (i.e. stores a table of facts).

Parameters :

• *formula ( Formula ) – A variable length argument list that accepts any number of input formulae objects as arguments.

• name ( str , optional ) – A custom name for the node to be used for identification and custom printing. If unspecified, defaults the structure of the node.

• activation ( dict , optional ) –

  Parameters given as a dictionary of configuration options, see the neural configuration for more details

Examples

# Propositional
A, B, C = Propositions('A', 'B', 'C')
Or(A, B, C)

# First-order logic
x, y = Variables('x', 'y')
A, C = Predicates('A', 'C')
B = Predicate('B', arity=2)
Or(A(x), B(x, y), C(y)))

class lnn. Predicate ( name : str , arity : int = 1 , ** kwds )

Creates a container for a predicate

Stores a table of truths, with columns specified by the arity and rows indexed by the grounding

Parameters :

• name ( str ) – name of the predicate

• arity ( int , optional ) – If unspecified, assumes a unary predicate

Examples

P1 = Predicate('P1')
P2 = Predicate('P2', arity=2)

add_data ( facts : Union [ dict , set ] )

Populate predicate with facts

Facts required in dict or set - dict for grounding-based facts - set for broadcasting facts across all groundings requires a set of 1 item dict keys for groundings and values as facts tuple facts required in bounds form (Lower, Upper)

lnn. Predicates ( * predicates : str , ** kwds )

Instantiates multiple predicates.

Examples

P1, P2 = Predicates("P1", "P2", arity=2)

class lnn. Proposition ( name : str , ** kwds )

Creates propositional containers

Stores and retrieves single truth bounds instead of tables as in FOL case

Parameters :

name ( str ) – name of the proposition

Examples

P = Proposition('Person')

add_data ( fact : Union [ Fact , bool ] )

Populate proposition with facts

Facts required in bool, tuple or None None fact assumes Unknown tuple fact required in bounds form (Lower, Upper)

lnn. Propositions ( * propositions : str , ** kwds )

Instantiates multiple propositions.

Examples

P1, P2 = Propositions("P1", "P2")

class lnn. Variable ( name : str , type : Optional [ str ] = None )

Free variables to quantify first-order logic formulae

Parameters :

• name ( str ) – name of the free variable

• type ( str , optional ) – constant of the type associated with the free variable

Examples

x = Variable('x', 'person')

lnn. Variables ( * variables : str , ** kwds ) → Union [ Variable , Tuple [ Variable , ... ] ]

Instantiates multiple variables.

Examples

x, y = Variables("x", "y")

class lnn. World ( value )

An enumeration for world assumptions to for incomplete knowledge.

See the discussion of OPEN vs CLOSED world assumptions for more information.

Parameters :

• AXIOM – Formulae that follow assumptions of universally being TRUE

• CONTRADICTION – Formulae that are in a contradictory state

• CLOSED – Formulae that follow the closed world assumption

• FALSE – Alias for CLOSED

• OPEN – Formulae that follow the open world assumption

class lnn. XOr ( * formula , ** kwds )

Symbolic nAry Exclusive or .

Returns a logical exclusive disjunction node where inputs can be propositions , called first-order logic predicates or any other connective formulae . Propositional inputs yield a propositional node, whereas if any input is a predicate it will cause the connective to increase its dimension to also be a FOL node (i.e. stores a table of facts).

Parameters :

• *formula ( Formula ) – A variable length argument list that accepts any number of input formulae objects as arguments.

• name ( str , optional ) – A custom name for the node to be used for identification and custom printing. If unspecified, defaults the structure of the node.

• activation ( dict , optional ) –

  Parameters given as a dictionary of configuration options, see the neural configuration for more details

Examples

# Propositional
A, B, C = Propositions('A', 'B', 'C')
XOr(A, B, C)

# First-order logic
x, y = Variables('x', 'y')
A, C = Predicates('A', 'C')
B = Predicate('B', arity=2)
XOr(A(x), B(x, y), C(y)))

downward ( index : Optional [ int ] = None , groundings : Optional [ Set [ Union [ str , Tuple [ str , ... ] ] ] ] = None , ** kwds ) → float

Downward inference from the operator to the operands.

Parameters :

• index ( int , optional ) – restricts downward inference to an operand at the specified index. If unspecified, all operands are updated.

• groundings ( str or tuple of str , optional ) – restrict upward inference to a specific grounding or row in the truth table

Returns :

tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step.

Return type :

float

upward ( groundings : Optional [ Set [ Union [ str , Tuple [ str , ... ] ] ] ] = None , ** kwds ) → float

Upward inference from the operands to the operator.

Parameters :

groundings ( str or tuple of str ) – restrict upward inference to a specific grounding or row in the truth table

Returns :

tightened_bounds – The amount of bounds tightening or new information that is leaned by the inference step.

Return type :

float

lnn. predicate_truth_table ( "p" , "q" , "r" , model=model )

randomises the truth table into a predicate by str(int) rows

Returns :

model

Return type :

Model

lnn. pretty_truth_table ( formulae : dict , unique_groundings : Optional [ List [ str ] ] = None ) → None

:param : :type : param formulae: Formulae is a dictionary with str:formula format ;i.e {“P or Q”: <lnn.symbolic.logic.n_ary_neuron >} :param : :type : param arity: The number of variables specified :param : :type : param unique_groundings: unique_groundings: Unique groundings that fill either the rows or columns i.e [“F”, “U”, “T”]

Return type :

A pretty truth table