How to use pmlayer.torch.layers.HLattice
In this tutorial, we demonstrate how to use pmlayer.torch.layers.HLattice.
The source code used in this tutorial is available at github.
You can construct a model that consists of a single HLattice layer by using the following code.
from pmlayer.torch.layers import HLattice
lattice_sizes = torch.tensor([4,4], dtype=torch.long)
model = HLattice(2,lattice_sizes,[0,1])
In this example, the first argument of HLattice specifies that this model receives a two-dimensional input.
The second argument specifies that the granularity of lattice is 4 for both inputs.
The third argument specifies that the output value is monotonically increasing with respect to both of the input features.
We can train this model by using a standard training method for PyTorch models as shown in the following code.
# prepare data
a = np.linspace(0.0, 1.0, 10)
x1, x2 = np.meshgrid(a, a)
y = (x1*x1 + x2*x2) / 2.0
x = np.concatenate([x1.reshape(-1,1),x2.reshape(-1,1)], 1)
data_x = torch.from_numpy(x.astype(np.float32)).clone()
data_y = torch.from_numpy(y.reshape(-1,1).astype(np.float32)).clone()
# train model
loss_function = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)
for epoch in range(5000):
pred_y = model(data_x)
loss = loss_function(pred_y, data_y)
model.zero_grad()
loss.backward()
optimizer.step()
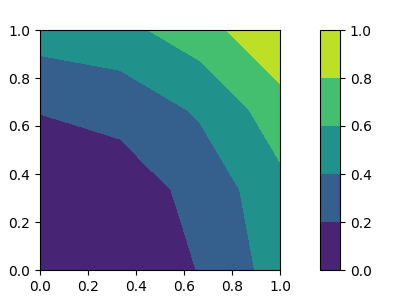
By using the following code, you can see that the model is appropriately trained to learn the function \(f(x,y) = (x^2 + y^2)/2\).
# plot
pred_y_np = pred_y.to('cpu').detach().numpy().copy().reshape(x1.shape)
plt.figure(figsize=(4,3))
ax = plt.subplot(1, 1, 1)
im = ax.contourf(x1, x2, pred_y_np, levels=[0.0,0.2,0.4,0.6,0.8,1.0])
plt.subplots_adjust(left=0.1, bottom=0.1, right=0.7, top=0.9)
cax = plt.axes([0.8, 0.1, 0.05, 0.8])
plt.colorbar(im,cax=cax)
plt.show()
We note that this layer constructs a \(k \times k\) grid internally, where \(k \geq 2\) is the hyperparameter used to specify the granularity of the grid.
In this tutorial, we used \(k=4\) and the following figure shows the grid.
In the internal structure of HLattice, each vertex of the grid is trained to learn the value \(f(x',y')\) of the input function \(f\), where \((x',y')\) is the coordinate of the vertex, while satisfying the monotonicity constraints.